Units & Notation

Concentration is the general term used to describe the amount of a specific substance in a given volume or mass of another substance.

It can be expressed in a range of units depending on the context, but in all cases it is calculated from the amount of the specific substance divided by the volume or mass of the other substance i.e.

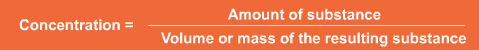
Concentration is equal to amount of substance divided by mass or volume of resulting substance

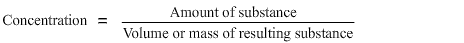
Square brackets round a substance are used to express its concentration e.g. [NaCl]

Some of the most common units are discussed below.

In some cases molarity is used in calculating concentrations. A mole is one gram molecular weight of an element or compound. Hence, to convert between grams and moles:

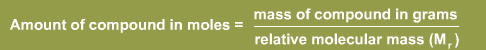
Amount of compound in moles is equal to mass of compound in grams divided by relative molecular mass

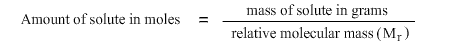
The above can also be expressed as:

Mass of compound in grams is equal to amount of compound in moles multiplied by relative molecular mass of the compound

Mass of compound in grams = amount of compound in moles × relative molecular mass (M_r)

If you are not sure how the equation highlighted in green has been re-arranged to get the equation highlighted in blue, then view the video below. Otherwise, you can go to another section of this resource.

This video contains sound.

The reason why the above equation has been re-arranged is because in some situations you have an amount of a compound in moles and its molecular weight and you need to find out the mass of the compound in grams. The process of re-arranging the equation is given below in detail.

In the original equation, amount of compound in moles is called the subject of the equation. To find mass of compound in grams, we need to rearrange the equation to make it the subject of the equation. We need to perform an arithmetic operation i.e. addition, subtraction, multiplication or division. We must do this to both sides of the equation in order to isolate mass of compound and separate it from relative molecular mass.

We will multiply both sides of the equation by relative molecular mass. The reason why both sides of the equation are being multiplied by relative molecular mass is because if we divide, multiply, add or subtract one side of the equation with a certain number, then we have to do a similar operation on the other side of the equation in order to balance it. This can be explained by likening the equation to a see-saw hanging in balance by two people of equal weights sitting on the opposite ends. If we double the number of people on one side of the see-saw, the see-saw will cease to remain in balance. To balance the see-saw again, we need to double the number of people of similar amount of weight on the other side as well. It was for this reason that we have multiplied the left hand side of the equation by relative molecular mass as well. Therefore the equation becomes:

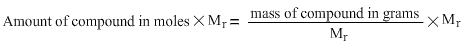
Amount of compound in moles times relative molecular mass is equal to mass of compound in grams divided by relative molecular mass and multiplied by relative molecular mass.

Lets look at the effect on the right hand side of the equation.

Relative molecular mass divided by relative molecular mass gives us 1. 1 multiplied by mass of compound in grams is mass of compound so we now have just the mass of compound in grams on the right hand side of the equation. The equation now looks as follows:

Amount of compound in moles × M_r = mass of compound in grams

Going back to the see-saw, if we flip the see-saw, it doesn't affect its balance. Similarly we can swap the sides of the above equation to give us:

Mass of compound in grams = amount of compound in moles × M_r

As can be seen, Mass of compound is now the subject of the equation.