Making solutions

Diluting solutions
Back to normal view | Send this page to printer

Save Trees. Print only when necessary.

Serial dilution

Print

Example

You are given a test tube containing 10 mL of a solution with 5 × 106 cells/mL. What is the concentration after three 1:10 dilutions?

The video below shows the systematic approach to solving the above problem.

Audio icon This video contains sound.



The first step is to extract from the problem statement the information that has been provided and the information being asked for.

The information we are provided with is:

We have a solution measuring 10 mL.

The concentration of this solution is 5 × 106 cells/mL.

This solution is applied a series of three 1:10 dilutions.

The information we are required to find is:

Concentration of the solution after three serial dilutions.

The second step is to identify the formula to find out the information being asked for.

As three 1 in 10 dilutions are going to take place, we can use this information to calculate the final dilution factor. We have got the initial concentration as well. Dilution factor and Initial concentration can be used to find the final concentration using the formula:

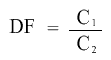
Dilution factor is equal to C1 divided by C2

where C1 is Initial concentration and C2 is Final concentration.

The third step is to match the information provided in the problem statement with the formula.

Dilution Factor needs to be calculated. C1 is 5 × 106 cells/mL. C2 needs to be found as well. So the equation becomes:

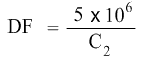
Dilution factor is equal to (5 times 10 to the power of 6) divided by C2

Lets calculate the Dilution Factor (DF) first.

As a series of three 1:10 dilutions are taking place, the dilution factor will be the product of dilution factor at each step i.e.

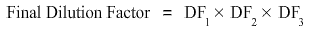
final dilution factor is equal to DF1 times DF2 times DF3

Hence final dilution factor is equal to 10 times 10 times 10 which is equal to 1000.

So the equation becomes:

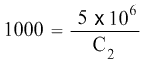
1000 is equal to (5 times 10 to the power of 6) divided by C2

With these values, we can now find the Final concentration C2.

The fourth step is to ensure that the information being used in the formula is in the correct units.

In this formula it is not important which units are used for C1 and C2, but it is important that the same units are used for C1 and C2. As C2 needs to be found out, therefore it doesn�t matter whichever units C1 is in. So, we now go ahead with the calculations.

We will multiply both sides of the equation with C2.

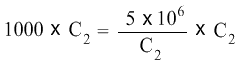
1000 times C2 is equal to ((5 times 10 to the power of 6) divided by C2) times C2

C2 cancels C2 on the right hand side of the equation, and the equation becomes:

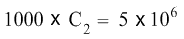
1000 times C2 is equal to 5 times 10 to the power of 6

To isolate C2 on the left hand side of the equation, we now divide both sides of the equation with the number 1000.

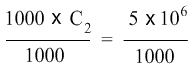
(1000 times C2) divided by 1000 is equal to (5 times 10 to the power of 6) divided by 1000

1000 cancels 1000 on the left hand side and on the right hand side, 5× 106, which can also be written as 5 × 1000000, when divided by 1000 gives 5 × 1000 or 5 × 103. So the equation becomes:

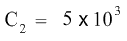
C2 is equal to 5 times 10 to the power of 6

Do not forget to add units to the answer. The concentration just determined has the same units as C1 i.e. cells/mL so the answer is 5x103 cells/mL.