- Units & Notation
- Moles per litre
- Grams per litre
- Percent solutions
- Parts per million
- Practice problems
Dilution
Example
10 mL of a 0.5 M CuSO4 solution is made up to 100mL with distilled water. What is the concentration of the resulting solution?
The video below shows the systematic approach to solving the above problem.
![]() This video contains sound.
This video contains sound.
We have certain amount of Copper Sulphate solution with a concentration of 0.5 Molar. 10 mL of this solution is diluted with 90 mL of distilled water to give resulting volume of 100 mL. This is 1 in 10 dilution.
The first step is to extract from the problem statement the information that has been provided and the information being asked for.
The information that has been provided is:
We took 10 mL of a solution with a concentration of 0.5 Molar. This solution is diluted to make a volume of 100 mL. So 10 mL can be termed as initial volume or Vinitial and the concentration of this 10 mL solution can be called initial concentration or Cinitial. Similarly, the volume of solution after dilution can be called final volume of the solution or Vfinal.
The information asked for is:
Concentration of the solution upon further dilution. This can be called C final (Cfinal)
The second step is to identify the formula to calculate the concentration of solution upon further dilution.
The formula to calculate Molarity or concentration is:
Molarity = Amount of solute in moles / Volume of solution in litres
The third step is to match the information provided in the problem statement with the formula.
Here we only have Vfinal or volume of the solution upon further dilution. This is 100 mL. So the equation becomes:
Molarity (Cfinal) = Amount of solute in moles / 100
In order to find Molarity, we need to have the amount of solute in moles. In this example, the amount of solute in the 10 mL solution remains the same when this 10 mL is diluted with distilled water to make 100 mL. In other words, the amount of solute remains the same before and after dilution. We know that the initial volume is 10 mL and the initial concentration or molarity is 0.5 Moles. Using these values, we can calculate the amount of solute through the formula:
Molarity = amount of solute in moles / volume of solution in litres
Placing values in the formula we get,
0.5 = Amount of solute in moles / 10 mL
Before going ahead with the calculations, it�s important to ensure that the information being used in the formula is in the correct units. When calculating concentration, molarity should always be in Molar, the solute should always be in moles and volume of the solution should always be in litres. In this case, molarity is in correct units, the amount of solute needs to be found out so we won�t worry about its units. However the volume of solution is in millilitres and we need to convert this in litres.
1000 millilitres = 1 litre
Therefore 1 millilitre = 1/1000 litres
and 10 millilitres = 1/1000 x 10 litres = 0.01 litres
The equation becomes:
0.5 = amount of solute in moles / 0.01
To isolate amount of solute on the right hand side and isolate it from the number 100, we multiply both sides of the equation by 0.01 giving us:
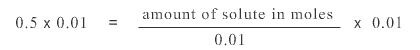
0.01 cancels 0.01 on the right hand side of the equation and on the left hand side of the equation 0.5 x 0.01 gives 0.005. The equation becomes:
0.005 = amount of solute in moles
This is the same as:
amount of solute in moles = 0.005
Now we have both pieces of information to find the concentration of the diluted solution i.e. Cfinal. Placing the values in the formula we get:
Molarity = 0.005 Moles / 100 millilitres
The fourth step is to see that the values are in the correct units. Again as before, the solute should always be in moles and volume of the solution should always be in litres. In this case, the amount of solute needs to be found out so we won�t worry about its units. However the volume of solution is in millilitres and we need to find this in litres. We know that:
1000 millilitres = 1 litre
Therefore 1 millilitre = 1/1000 litres
and 100 millilitres = 1/1000 x 100 litres = 0.1 litres
The equation now becomes:
Molarity = 0.005 moles / 0.1 litres
0.005 divided by 0.1 gives us 0.05 hence the concentration of the diluted solution is 0.05.
Do not forget to add units to the answer. The concentration of solution is M, hence the answer is 0.05 M.
An alternative approach to solving the above problem is as follows:
Remembering molarity is the number of moles of substance needed for each litre of solution, use a proportion calculation:
Original 0.5 M solution means

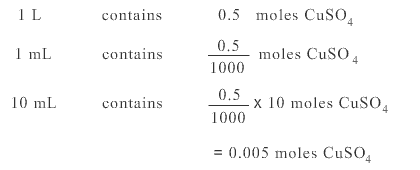
Diluted solution contains 0.005 moles in 100 mL
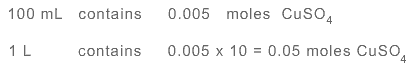
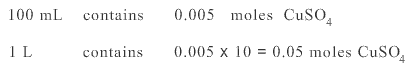
Hence molarity of diluted solution is 0.05 M.